D é n e s T a m á s matematikus
e-mail: tdenest@freemail.hu
![]()
Latin és bűvös négyzetek a játékos alkalmazásoktól az
űrtávközlésig
Nem
egyedülálló a matematika történetében, hogy egyes fejezetei a szórakozás, a játék
területén fogantak és hosszabb-rövidebb fejlődés után a matematika új
fejezeteivé váltak. Ezt az utat járta be a kombinatorika egy alig 300 éves
fejezete, a latin négyzetek elmélete. Különössége mégsem abban áll, hogy
fejlődésének és főleg alkalmazásainak jelentős része a XX. század gyümölcse,
hanem abban, hogy a klasszikus numerikus gondolkodást felcserélte a struktúrák
belső összefüggéseinek elemzésével és igen szemléletes ábrázolásával.
Jelen
dolgozatomban a latin négyzetek szerteágazó, klasszikus és egészen modern
alkalmazásainak és lehetőségeinek vázlatos bemutatását tűztem ki célul, a
szórakoztató matematikától, a XXI. század információs társadalmában kulcs
jelentőségű adatátvitelen keresztül, a kriptográfiáig[1].
Alapfogalmak és definíciók történeti illusztrációkba
ágyazva
Mivel a latin négyzetek elmélete egyelőre nem képezi matematika oktatásunk törzsanyagát, így a jelen dolgozat megértéséhez az olvasónak néhány alapfogalom megismerésére lesz szüksége. Ezeket az alapvető fogalmakat és összefüggéseket, valamint a keletkezésük történeti hátterét ismertetem vázlatosan a következőkben.
Egy n-ed rendű latin négyzeten egy olyan n x n méretű négyzetes mátrixot értünk, amelynek soraiban és oszlopaiban az a1, a2,………,an elemek mindegyike pontosan egyszer szerepel. Általában az a1, a2,………,an elemek az 1,2,……,n természetes számok. Az 1/a., 1/b.ábra példát mutat egy-egy 4-ed rendű latin négyzetre.
|
1 |
2 |
3 |
4 |
|
2 |
3 |
4 |
1 |
|
3 |
4 |
1 |
2 |
|
4 |
1 |
2 |
3 |
1/a. ábra
|
1 |
2 |
3 |
4 |
|
2 |
1 |
4 |
3 |
|
3 |
4 |
1 |
2 |
|
4 |
3 |
2 |
1 |
1/b.ábra
A definícióból világosan kiderül, hogy jelen esetben nem az a1, a2,………,an elemek számértéke számít, csupán csak különbözőségük, valamint a mátrixban elfoglalt helyük (struktúrájuk).
Egy latin négyzetet ciklikusnak nevezünk, ha egymás alatti soraiban az elemek sorrendje azonos, csak egy hellyel jobbra (vagy balra) vannak az elemek eltolva (lásd 1/b.ábra).
Egy n-ed rendű latin négyzet egy tranzverzálisán értjük n darab olyan elemét, amelyek mindegyike különböző sorában, illetve oszlopában helyezkedik el és nincs köztük két azonos. Az 1/a. ábrán látható latin négyzetben a satírozott négy elem például egy tranzverzálist alkot.
Két n-ed rendű latin négyzetet akkor nevezünk ortogonálisnak, ha egymásra helyezve őket, az egymás felett levő elemekből alkotott párok mind különbözőek. Példaképpen bemutatjuk az l/a. ábrán szereplő latin négyzet egy ortogonális párját (lásd 2.ábra), majd a két latin négyzet egymásra helyezésével nyert számpárokat. (Az olvasó a 3.ábra segítségével könnyen meggyőződhet arról, hogy a 16 számpár mind különböző.)
|
1 |
2 |
3 |
4 |
|
4 |
3 |
2 |
1 |
|
2 |
1 |
4 |
3 |
|
3 |
4 |
1 |
2 |
2.ábra
|
1,1 |
2,2 |
3,3 |
4,4 |
|
2,4 |
1,3 |
4,2 |
3,1 |
|
3,2 |
4,1 |
1,4 |
2,3 |
|
4,3 |
3,4 |
2,1 |
1,2 |
3. ábra
Az ortogonális latin
négyzet párok létezése, mint látni fogjuk, szoros kapcsolatban van a
tranzverzálisokkal. Erre vonatkozó alapvető eredmény Dulmage-Mendelshon tétele:
Két n-ed rendű latin
négyzet ortogonalitásának szükséges és elégséges feltétele, hogy a diszjunkt
diagonálisaik száma pontosan n legyen.
L1, L2,….,Lk
n-ed rendű latin négyzetek egy ortogonális rendszert alkotnak, ha
bármely két különböző latin négyzetet véve a k darab közül, azok
ortogonális párt képeznek. Bebizonyítható, hogy nxn-es latin
négyzetekből legfeljebb n-1 olyan létezhet, amelyek közül bármely kettő
ortogonális, ha viszont ezek mind léteznek, akkor az ortogonális latin
négyzetek teljes rendszeréről beszélünk. A XX. század elején
kiderült, hogy számos súlyos kombinatorikai probléma mélyén az ilyen rendszerek
létezésének kérdése rejlik.
![]() Egy L latin négyzetet akkor nevezünk vízszintesen teljesnek,
ha bármely a latin négyzetben szereplő a, b elempárra van olyan sora
L-nek, amelyben az a elemet b követi. (Ha a leírt tulajdonság
oszlop irányban teljesül, akkor az L latin négyzetet függőlegesen
teljesnek nevezzük.) Egy latin négyzetet, amely vízszintesen és függőlegesen
is teljes, teljes latin négyzetnek nevezzük. A 4. ábrán látható latin
négyzet teljes (erről meggyőződhet az olvasó, ha a kívánt tulajdonságot megvizsgálja
az összes lehetséges (1,2), (1,3), (1,4), (2,3), (2,4), (3,4) elempárokra).
Egy L latin négyzetet akkor nevezünk vízszintesen teljesnek,
ha bármely a latin négyzetben szereplő a, b elempárra van olyan sora
L-nek, amelyben az a elemet b követi. (Ha a leírt tulajdonság
oszlop irányban teljesül, akkor az L latin négyzetet függőlegesen
teljesnek nevezzük.) Egy latin négyzetet, amely vízszintesen és függőlegesen
is teljes, teljes latin négyzetnek nevezzük. A 4. ábrán látható latin
négyzet teljes (erről meggyőződhet az olvasó, ha a kívánt tulajdonságot megvizsgálja
az összes lehetséges (1,2), (1,3), (1,4), (2,3), (2,4), (3,4) elempárokra).
|
4 |
1 |
3 |
2 |
|
3 |
4 |
2 |
1 |
|
1 |
2 |
4 |
3 |
|
2 |
3 |
1 |
4 |
4. ábra
Kártyalapok és a 36
tiszt problémája
Leonhard Euler (1707-1783)
a XVIII. századi matematika egyik óriása a latin négyzetek névadója, mivel Ő
alkalmazott a négyzetes mátrixbeli elemek jelölésére latin betűket, az addig
szokásos számok helyett. Ez az algebrai struktúrák területén hasonló
jelentőséggel bírt, mint F. Viéte (1540-1603) 200 évvel korábbi tette, az
algebrai egyenletek szimbólumainak bevezetésével. L. Eulert szokták említeni,
mint aki bevezette az ortogonális latin négyzet párok fogalmát is. Azonban már
Eulert megelőzően is ismerték az Eulernek tulajdonított két fogalmat. Szeretném
a történelmi hűség kedvéért az olvasó figyelmét Claude-Gaspar Bachet de
Méziriac-ra (1581-1638) M. Ozanam-ra (1640-1712) felhívni, akik már Euler előtt
is játék kártyával kapcsolatosan jutottak a latin négyzetek, illetve ezekből
alkotott ortogonális párok fogalmához. (lásd [1], [9], [10]). Az 5/a. ábrán
látható negyed rendű ortogonális latin négyzet pár [1]-ből való, amely
tulajdonképpen a következő feladatot oldja meg: hogyan lehet a römi kártya
négy színű (coeur, treffe, carreau, pique) figuráiból (ae, roi, dame, valet) 16
lapot úgy kiválasztani és egy 4x4 méretű mátrixban elrendezni, hogy minden szín
minden figurával előforduljon és minden sorban, illetve oszlopban minden szín
és minden figura pontosan egyszer forduljon elő.
|
AS DE
COEUR |
ROI DE TREFLE |
DAME DE
CARREAU |
VALET DE
PIQUE |
|
VALET DE CARREAU |
DAME DE
PIQUE |
ROI DE
COEUR |
AS DE
TREFLE |
|
ROI DE PIQUE |
AS DE CARREAU |
VALET DE TREFLE |
DAME DE
COEUR |
|
DAME DE TREFLE |
VALET DE COEUR |
AS DE
PIQUE |
ROI DE
CARREAU |
5/a. ábra
Ugyanennek a feladatnak a
magyar kártyákkal történő megoldását mutatjuk be az 5/b. ábrán.

5/b. ábra
Később 1776-ban majd
1779-ben Euler a Szent Pétervári Akadémián tartott előadásában már megmutatta,
hogy ha n 4-gyel osztható természetes szám, akkor van n-ed rendű latin
négyzetekből álló ortogonális pár. Ugyancsak ekkor felvetette az azóta 36
tiszt problémájaként ismert feladatot: Válasszunk ki 36 tisztet úgy,
hogy közöttük hat különböző rendfokozatú szerepeljen és a tisztek hat különböző
csapattestből kerüljenek kiválasztásra, minden egyes csapattestből hat
különböző rendfokozatú tiszt szerepeljen a 36 között. Fel lehet-e a fentiek
szerint kiválasztott tiszteket úgy állítani egy 6 x 6-os alakzatba, hogy minden
egyes sorban illetve oszlopban minden rendfokozat illetve csapattest pontosan
egyszer szerepeljen. A kérdés röviden úgy is feltehető, hogy létezik-e két
olyan hatod rendű latin négyzet, amely egymásra ortogonális?
A feladat kísértetiesen hasonlít az előzőkben a römi, illetve magyar kártyákkal megoldottakhoz, mégis Euler azt sejtette, hogy a 36 tiszt problémájának nincs megoldása. Sőt ennél általánosabban azt is sejtette, hogy általában ha n=4k+2 alakú, akkor nincsen ortogonális n-ed rendű latin négyzet pár. Ez utóbbi sejtést évszázadokon át Euler sejtésnek hívták és több mint 200 évig foglalkoztatta a matematikusokat a sejtés bizonyítása, vagy cáfolása.
Az Euler sejtés megcáfolása és néhány megoldatlan probléma
Már Euler tudta, hogy sejtése az n = 2 esetre igaz (a bizonyítás igen egyszerű, hiszen az 1, 2 számokból mindössze két különböző 2x2-es latin négyzet készíthető). Az n = 6 esetre, azaz a 36 tiszt problémájára azonban a bizonyítással több mint 100 évet kellett várni, míg G. Tarry éppen a XX. század fordulóján, 1900-ban bebizonyította. Euler általános sejtése azonban nem bizonyult igaznak. Csaknem kétszáz évvel a sejtés megfogalmazása után, 1959-ben egy igen bonyolult bizonyítással R.C. Bose, S.S. Shrikhande és E.T. Parker bebizonyították, hogy az Euler sejtés nem igaz, ha n nagyobb mint 10, azaz minden n=4k+2 alakú számra, ha k értéke legalább 2, léteznek ortogonális latin négyzetek.
Az alábbi 6.ábra szemlélteti azt a híres tizedrendű ortogonális latin négyzet párt, amelyet 1959-ben hoztak nyilvánosságra, megdöntve az Euler sejtést az n=10 esetre:
|
0 |
4 |
1 |
7 |
2 |
9 |
8 |
3 |
6 |
5 |
|
8 |
1 |
5 |
2 |
7 |
3 |
9 |
4 |
0 |
6 |
|
9 |
8 |
2 |
6 |
3 |
7 |
4 |
5 |
1 |
0 |
|
5 |
9 |
8 |
3 |
0 |
4 |
7 |
6 |
2 |
1 |
|
7 |
6 |
9 |
8 |
4 |
1 |
5 |
0 |
3 |
2 |
|
6 |
7 |
0 |
9 |
8 |
5 |
2 |
1 |
4 |
3 |
|
3 |
0 |
7 |
1 |
9 |
8 |
6 |
2 |
5 |
4 |
|
1 |
2 |
3 |
4 |
5 |
6 |
0 |
7 |
8 |
9 |
|
2 |
3 |
4 |
5 |
6 |
0 |
1 |
8 |
9 |
7 |
|
4 |
5 |
6 |
0 |
1 |
2 |
3 |
9 |
7 |
8 |
|
0 |
7 |
8 |
6 |
9 |
3 |
5 |
4 |
1 |
2 |
|
6 |
1 |
7 |
8 |
0 |
9 |
4 |
5 |
2 |
3 |
|
5 |
0 |
2 |
7 |
8 |
1 |
9 |
6 |
3 |
4 |
|
9 |
6 |
1 |
3 |
7 |
8 |
2 |
0 |
4 |
5 |
|
3 |
9 |
0 |
2 |
4 |
7 |
8 |
1 |
5 |
6 |
|
8 |
4 |
9 |
1 |
3 |
5 |
7 |
2 |
6 |
0 |
|
7 |
8 |
5 |
9 |
2 |
4 |
6 |
3 |
0 |
1 |
|
4 |
5 |
6 |
0 |
1 |
2 |
3 |
7 |
8 |
9 |
|
1 |
2 |
3 |
4 |
5 |
6 |
0 |
9 |
7 |
8 |
|
2 |
3 |
4 |
5 |
6 |
0 |
1 |
8 |
9 |
7 |
6.ábra
Mint említettem már, ismeretes az a tétel, hogy egy n-ed rendű latin négyzetekből álló ortogonális rendszerben legfeljebb n-1 latin négyzet lehet. Azonban nagyon keveset tudunk arról, hogy ez a felső korlát mikor érhető el. Tudjuk, hogy ha n prímszám hatvány, akkor van teljes n-ed rendű ortogonális rendszer. Az n=22 esetre példa a 7.ábrán látható három latin négyzetből álló negyedrendű ortogonális rendszer:
|
0 |
1 |
2 |
3 |
|
1 |
0 |
3 |
2 |
|
2 |
3 |
0 |
1 |
|
3 |
2 |
1 |
0 |
|
0 |
1 |
2 |
3 |
|
2 |
3 |
0 |
1 |
|
3 |
2 |
1 |
0 |
|
1 |
0 |
3 |
2 |
|
0 |
1 |
2 |
3 |
|
3 |
2 |
1 |
0 |
|
1 |
0 |
3 |
2 |
|
2 |
3 |
0 |
1 |
7.ábra
Nem sikerült azonban teljes n-ed rendű latin négyzetből álló ortogonális rendszert találni, ha n nem prímszám hatvány. Azonban R. H. Bruck és H. J. Ryser bebizonyították a következő tételt: n-1 darab n-ed rendű latin négyzetből álló ortogonális rendszer nem létezik, ha n néggyel osztva 1, illetve 2 maradékot ad, hacsak nem n = a2 + b2 (n két négyzetszám összegeként előállítható). Itt érdemes megjegyezni, hogy Fermat híres karácsonyi tétele, melyet 1640. karácsonyán egy M. Mersenne-nek írt levelében fogalmazott meg, így szól: Minden n=4k+1 alakú prímszám felírható két egész szám négyzetének összegeként. E két tétel összevetéséből tehát az következik, hogy ha n 4k+1 alakú prímszám, akkor létezik n-1 darab (azaz 4k darab) latin négyzetből álló (azaz teljes) ortogonális rendszer.
Ha N(n) jelöli az n-ed rendű latin négyzetekből
álló ortogonális rendszerben lévő latin négyzetek számát, akkor nyilvánvaló
az előbbiek alapján, hogy N(n) nagyobb vagy egyenlő mint
n-1. S. Chowle., P. Erdős és E.G. Straus bebizonyították, ha n
elég nagy, akkor fenn áll, hogy
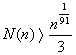 , majd R. M. Wilsonnak sikerült bebizonyítani, hogy nagy n értékekre
, majd R. M. Wilsonnak sikerült bebizonyítani, hogy nagy n értékekre
![]() .
.
A
latin és bűvös négyzetek kapcsolata
n-ed rendű bűvös négyzetnek nevezünk egy olyan négyzetes mátrixbeli elrendezést, amelyben n2 egész szám szerepel (általában, de nem szükségszerűen 0,1,………..,n2) és a négyzetes mátrix minden sorában, oszlopában, illetve két fő átlójában az elemek összege azonos.
Lo Shu bűvös négyzet
Talán nem véletlen, hogy a bűvös négyzetek, akárcsak a számmisztika, már jóval korábban, az ókori Kínában felbukkant. A Lo Shu négyzet az ókori Kínából származó bűvös négyzet, melyet egy óriásteknős páncéljára festettek és a Feng Sui fontos részét képezi (lásd a 8. ábrát).
|
4 |
9 |
2 |
|
3 |
5 |
7 |
|
8 |
1 |
6 |
8.ábra A Lo Shu bűvös négyzet
ókori alakja teknősre festve és mai alakjában mátrixba rendezve
|
SUN (Szél) DÉLKELET |
LI (Napsugár) DÉL |
KUN (Föld) DÉLNYUGAT |
|
CHEN (Villám) KELET |
|
TUI (Tó) NYUGAT |
|
KEN (Hegység) ÉSZAKKELET |
K’AN (Hold) ÉSZAK |
CHIEN (Menyország) ÉSZAKNYUGAT |
9.ábra A Lo Shu bűvös négyzet és a Feng Sui
A Lo Shu négyzetben a páratlan számok
szerepe a férfi (yang), míg a páros számoké a nő (yin). Az 1-es szám minden dolgok kezdete, a 9-es
reprezentálja a teljességet, míg a centrumban elhelyezkedő 5-ös az erő, energia
jelképe. A 9.ábra mutatja az épület tájolásának meghatározását, illetve a
yin-yang változását az éves ciklusokban.
Bolyai János bűvös négyzete
Több évtizedes kutatás után 1999-ben jelent meg Kiss Elemér marosvásárhelyi matematika professzor és Bolyai kutató [8] kötete, melyben Bolyai Jánosról egy egészen új képet tárt elénk. Bolyai János kéziratos hagyatékának szisztematikus áttanulmányozása arra a meglepő eredményre vezetett, hogy Bolyai közismert geometriáján kívül, nagyrészt a matematika egészen más területeivel foglalkozott. Ezen eddig ismeretlen eredményei közül való, az alábbi 10.ábrán látható kézirat töredék, amely éppen a 3x3-as bűvös négyzetek általános leírásával foglalkozik. Mivel Kiss Elemér professzor igen alapos kutatásai ellenére sem találta meg ezen kézirat többi oldalát, e helyen szeretném rekonstruálni annak néhány lehetséges összefüggését. Mint látni fogjuk, a végeredmény meghökkentő összefüggést tár fel a fentiekben bemutatott Lo Shu bűvös négyzettel.

10.ábra Bolyai János 3x3-as bűvös négyzetekről szóló kézirat töredéke
A 10.ábra kéziratában Bolyai a-val jelölte a 3x3-as bűvös négyzet sor, oszlop és átló összegeit, a középső cella elemet b-vel, az első két cella elemeit x és y-nal jelölte. Így a 11.ábrán látható kitöltést kapjuk:
|
x |
y |
a-x-y |
|
2a-2b-2x-y |
b |
2x+y-a-b |
|
x+y+2b-a |
a-y-b |
a-x-b |
11.ábra
Írjuk fel a 11.ábra mátrixának mellékátlójára adódó egyenletet:
(1) a-x-y+b+x+y+2b-a=a amelyből kapjuk, hogy a=3b
ami éppen Bolyai kéziratának közepén található összefüggés. Ha pedig a cellákba a bűvös négyzet képzési szabályai szerint az 1, 2, 3, …, 9 számtani sorozatot írjuk, akkor fennáll:
(2) ![]()
Ekkor a 11.ábrába helyettesítve kapjuk:
|
x |
y |
15-x-y |
|
20-2x-y |
5 |
2x+y-10 |
|
x+y-5 |
10-y |
10-x |
12.ábra
(2)-ből tudjuk, hogy minden sor,
oszlop és átló elemeinek az összege 15. Mivel az 5-ös szám
középen van, így minden irányban a két mellette elhelyezkedő elem a 10-nek
egy-egy partíciója. Ezek: 1+9, 2+8,
3+7, 4+6
Mivel a cellákban csupa különböző szám áll, így a vízszintes, a függőleges és átlós irányú szomszédok éppen a 4 db partíciót alkotják. A négyből kettő szabadon választható, a másik kettő ezekből már adódik. Az összes megoldások száma tehát:
(3) ![]()
A megoldások a 12.ábrán szereplő mátrix elemeire felírt összefüggésekből levezethetők:
|
2 |
7 |
6 |
|
9 |
5 |
1 |
|
4 |
3 |
8 |
|
2 |
9 |
4 |
|
7 |
5 |
3 |
|
6 |
1 |
8 |
|
4 |
3 |
8 |
|
9 |
5 |
1 |
|
2 |
7 |
6 |
|
8 |
3 |
4 |
|
1 |
5 |
9 |
|
6 |
7 |
2 |
|
8 |
1 |
6 |
|
3 |
5 |
7 |
|
4 |
9 |
2 |
|
4 |
9 |
2 |
|
3 |
5 |
7 |
|
8 |
1 |
6 |
Bár nem tudjuk, hogy Bolyai a jegyzetei többi oldalán mit írhatott, de a 10.ábra rajza melletti megjegyzése pontos, miszerint ha ezt a számtani sorozatot alkalmazzuk a bűvös négyzet kitöltésére, akkor csupán egyetlen megoldás van. Ha ugyanis a fenti hat mátrixot megnézzük, azok a középső elem körüli elforgatásokkal egymásba átvihetők!
A Lo Shu bűvös négyzet pontosan megegyezik a Bolyai-féle hatodik megoldással. Vajon Bolyai János tudott erről?
Albrecht Dürer bűvös négyzete
Egy-egy bűvös négyzet összeállítása a matematika történetének hajnalán még igen nehéz feladatnak számított, ezért nem csodálkozhatunk, hogy azoknak valamilyen mágikus erőt tulajdonítottak. Az utóbbi századokban sokat foglalkoztak a bűvös négyzetek matematikai tulajdonságaival és kutatták készítésük módszereit.
Albrecht Dürernek, a reneszánsz kor nagy német festőjének a figyelmét is egy "többszörösen" bűvös négyzet ragadta meg, ezt láthatjuk Melankólia című rézmetszetének hátterében (lásd 13.ábra).


13.ábra Albrecht Dürer Melankólia című rézmetszetén szereplő bűvös négyzet
Ez a bűvös négyzet már Dürer korában több mint ezeréves múltra tekinthetett vissza, valószínűleg Indiából került át Európába. A művész a sorokat kissé átrendezte, hogy az alsó sor közepére a 15 és a 14 számok kerüljenek, jelezve műve készítésének évét, 1514-et. Dürer bűvös négyzete teljesen helytálló: mezőin az 1-tõl 16-ig terjedő egész számok helyezkednek el, soraiban, oszlopaiban és átlóiban a számok összege mindenütt 34, másrészt az említett dátumot adó két számon kívül több egyéb különlegessége is van. Alsó és felső sorában a számok négyzeteinek összege is egyenlő, és ugyanez áll a két szélső oszlop számaira is. A négyzetet függőleges és vízszintes középvonala négy darab 2x2-es négyzetre vágja szét, ezek mindegyikében ugyancsak 34 a számok összege, de ugyanannyi a középen elhelyezkedő 2x2-es négyzetben is. A négyzet négy csúcsánál levő számok összege is 34, s ugyanez áll azoknak a 3x3-as négyzeteknek a sarokszámaira is, amelyeket az eredetiből egy szélső sor és oszlop elhagyásával nyerünk.
Bűvös négyzet konstrukciók latin négyzetekből
A játékos elme bravúros teljesítménye a sakktáblára írt lóugrásos bűvös négyzet. Ezen ha a huszár elindul az 1-es számot tartalmazó mezőről (lásd a 14.ábra fekete mezőjét), bejárhatja a sakktáblát úgy, hogy mindegyik ugrása a következő számot tartalmazó mezőre vezet, ráadásul a 64. ugrás visszajuttathatja a kiindulási helyére. Bemutatunk egy ilyen sakktáblát, melynek minden sorában és oszlopában 260 a számok összege (az átlókra ez itt nem teljesül).
|
50 |
11 |
24 |
63 |
14 |
37 |
26 |
35 |
|
23 |
62 |
51 |
12 |
25 |
34 |
15 |
38 |
|
10 |
49 |
64 |
21 |
40 |
13 |
36 |
27 |
|
61 |
22 |
9 |
52 |
33 |
28 |
39 |
16 |
|
48 |
7 |
60 |
1 |
20 |
41 |
54 |
29 |
|
59 |
4 |
45 |
8 |
53 |
32 |
17 |
42 |
|
6 |
47 |
2 |
57 |
44 |
19 |
30 |
55 |
|
3 |
58 |
5 |
46 |
31 |
56 |
43 |
18 |
14.ábra Lóugrásos bűvös négyzet
A bűvös négyzetek megalkotásának ezen kívül még számos módját dolgozták ki. A játékos alkalmazásokon jóval túlmutató jelentősége van azonban a bűvös négyzetek és a latin négyzetek kapcsolatának. A 15.ábrán szereplő két latin négyzetről [5]-ben mutatta meg a szerző, hogy összegük egy bűvös négyzet, amit a 16.ábrán mutatunk be.
|
5 |
15 |
0 |
10 |
20 |
|
0 |
10 |
20 |
5 |
15 |
|
20 |
5 |
15 |
0 |
10 |
|
15 |
0 |
10 |
20 |
5 |
|
10 |
20 |
5 |
15 |
0 |
+
|
5 |
3 |
1 |
4 |
2 |
|
4 |
2 |
5 |
3 |
1 |
|
3 |
1 |
4 |
2 |
5 |
|
2 |
5 |
3 |
1 |
4 |
|
1 |
4 |
2 |
5 |
3 |
15.ábra
|
10 |
18 |
1 |
14 |
22 |
|
4 |
12 |
25 |
8 |
16 |
|
23 |
6 |
19 |
2 |
15 |
|
17 |
5 |
13 |
21 |
9 |
|
11 |
24 |
7 |
20 |
3 |
16.ábra
Ez a speciális eset általánosítható a következő módon:
Ha n=2k+1 alakú páratlan szám, akkor létezik két n-ed rendű latin
négyzet (jelöljük ezeket L(aij) és L(bij)-vel), melyek
összege az M(cij) nxn-es
mátrix, melynek minden sorában, oszlopában és két főátlójában az elemek összege
![]() és az M(cij) mátrix elemei az 1, 2, …, n2 számtani sorozat
elemei.
és az M(cij) mátrix elemei az 1, 2, …, n2 számtani sorozat
elemei.
Bizonyításként bemutatjuk a két latin négyzet szerkesztési elvét.
Mivel L(aij) egy latin négyzet, így definíció szerint minden sorában és oszlopában az 1, 2, …, n egész számok egy-egy permutációját helyezzük el, így a sorokban, illetve oszlopokban lévő számok összege mindig
(4) ![]()
Az világos, hogy az előállítandó bűvös négyzet összes elemeinek összege
(5) 1+2+3+…+n2 = ![]()
(5)-ből következik, hogy a bűvös négyzet sor, illetve oszlop összegei:
(6) ![]()
Azaz (6)-ból (4)-et kivonva kapjuk az L(bij) latin négyzet sor, illetve oszlop összegeit:
(7) ![]()
Amennyiben feltételezzük, hogy L(bij) sorai és oszlopai is egy b1,b2,…,bn számtani sorozat elemeit tartalmazzák, úgy (7) alapján felírhatjuk a sorozat összegére vonatkozóan:
(8) ![]()
Legyen b1=0, ekkor bn=b1+(n-1)d=(n-1)d, ahol d jelöli a számtani sorozat differenciáját. Ezt (8)-al összevetve kapjuk:
(9) ![]()
|
5 |
3 |
1 |
4 |
2 |
|
4 |
2 |
5 |
3 |
1 |
|
3 |
1 |
4 |
2 |
5 |
|
2 |
5 |
3 |
1 |
4 |
|
1 |
4 |
2 |
5 |
3 |
=L(aij)
17.ábra
|
10 |
15 |
0 |
5 |
20 |
|
0 |
5 |
20 |
10 |
15 |
|
20 |
10 |
15 |
0 |
5 |
|
15 |
0 |
5 |
20 |
10 |
|
5 |
20 |
10 |
15 |
0 |
=L(bij)
18.ábra
|
15 |
18 |
1 |
9 |
22 |
|
4 |
7 |
25 |
13 |
16 |
|
23 |
11 |
19 |
2 |
10 |
|
17 |
5 |
8 |
21 |
14 |
|
6 |
24 |
12 |
20 |
3 |
=L(aij)+L(bij)=M(cij)
19.ábra
Az L(bij) latin négyzet elemei tehát a 0, n, 2n, …, n(n-1) számok lesznek, ahogy ezt a 18.ábra latin négyzeténél láthatjuk is. Most már csupán az a feladatunk, hogy ezeket a számokat a bűvös négyzet szabályit kielégítő módon elhelyezzük az L(bij) mátrixban!
Ehhez elsőként válasszuk ki az L(aij) latin négyzet egy tranzverzálisát (a 17. és 18.ábrán a kiválasztott tranzverzálisokat satírozással jelöltem, az azonos tranzverzálishoz tartozó elemek azonos szürkeárnyalattal szerepelnek a fehértől a feketéig), ez a definíció szerint az L(aij) mátrix minden sorából és oszlopából pontosan egy elemet tartalmaz, amelyek az 1,2,3,…,n számokból állnak. Ha tehát az L(bij) mátrixban ennek a tranzverzálisnak megfelelő helyek mindegyikére a 0 értéket írjuk, akkor az M(cij) mátrixban a cij=aij+bij elemek értékei, rendre az 1,2,3,…,n számok lesznek. Most keressünk az L(aij) latin négyzetben egy másik tranzverzálist és az ennek megfelelő helyekre írjuk az L(bij) mátrixban az n számot. Ekkor az M(cij) mátrixban a cij=aij+bij elemek rendre az n+1,n+2,n+3,…,2n értékeket veszik fel. Ezt az eljárást folytatva az L(aij) latin négyzet n darab tranzverzálisával, az eredmény M(cij) mátrix pontosan a kívánt 1, 2, 3, …, n2 számsorozat értékeit fogja tartalmazni és az L(bij) mátrix is egy latin négyzet lesz. Ezzel az állításunkban megfogalmazott összes feltételt teljesítettük, amit a fenti ábrákon lépésről-lépésre követhetünk.
A konstrukcióból egyértelműen adódik, hogy L(aij) és L(bij) ortogonális párok, ami egyúttal rámutat ilyen párok szerkesztésére is. Itt érzékelhetjük, hogy az ortogonális párok és a tranzverzálisok között milyen szoros kapcsolat van. Szükséges megjegyezni, hogy a fenti konstrukcióban kihasználtuk H.J. Ryser azon sejtését, amely szerint, ha n=2k+1 (n páratlan), akkor minden n-ed rendű latin négyzetben van tranzverzális. Ezt a sejtést kibővítettük azzal, hogy feltételeztük n darab tranzverzális létezését. Ennek általános érvényű bizonyítása még várat magára, de megmutatjuk, hogy a fenti bűvös négyzetek konstrukciójára vonatkozó algoritmusunk nem megalapozatlan, igaz ugyanis az alábbi tétel:
Ha egy n-ed rendű latin négyzet ciklikus, akkor létezik
benne n darab tranzverzális, amelyek
éppen a főátlóra vonatkozó tört diagonálisok elemei (a tranzverzálisok
azonos szürke árnyalattal vannak besatírozva az alábbi 20.ábrán).
|
1 |
2 |
3 |
4 |
5 |
|
2 |
3 |
4 |
5 |
1 |
|
3 |
4 |
5 |
1 |
2 |
|
4 |
5 |
1 |
2 |
3 |
|
5 |
1 |
2 |
3 |
4 |
20.ábra
A. H. Frost [5]-ben vizsgálta a Nasik négyzeteket, amelyek egy speciális osztályát adják a bűvös négyzeteknek. (Nevezetesen egy olyan bűvös négyzetet nevezünk Nasik négyzetnek, amelynek a tört diagonálisain fekvő elemek összege is a sorok, oszlopok, illetve fődiagonálisok elemeinek összegével azonos. Tört diagonálisnak nevezzük az nxn-es mátrix főátlóinak két oldalán, azzal párhuzamosan elhelyezkedő átlókat, amelyek össz elemszáma n. A 21.ábrán azonos satírozással és számozással jelöltem a törtátlókat.)
Frost olyan latin négyzeteket használt Nasik négyzetek szerkesztéséhez, amelyben az azonos elemek egymás utáni lóugrásokkal helyezhetők el. Konstrukcióját a 21. ábrán szerepeltetjük.
|
1 |
2 |
3 |
|
|
2 |
3 |
|
1 |
|
3 |
|
1 |
2 |
|
|
1 |
2 |
3 |
21. ábra
Végül a latin négyzetekkel való barátkozáshoz segítségül bemutatok egy latin négyzet társasjátékot. A játékot két játékos játsza, A és B (mindig A teszi meg az első lépést). A játékot egy n x n méretű üres táblán játsszák. Kezdéskor A egy 1 és n közötti számot a tábla tetszés szerinti helyére ír, majd B úgy ír a tábla még üres mezőire egy szintén 1 és n közötti számot, hogy az a latin négyzet tulajdonságának ne mondjon ellent (az ilyen lépéseket legálisnak nevezzük). Aki utoljára tud legális lépést a táblára írni, az nyer.
Egy 4x4-es táblán
lehetséges játékot mutatunk be a 22.ábrán. A fehér mezőkre írt számok A,
a szürke mezőkre írtak B lépéseit mutatják.
|
1 |
2 |
3 |
|
|
2 |
3 |
1 |
|
|
3 |
1 |
2 |
4 |
|
4 |
|
|
1 |
22. ábra A latin négyzet játék egy lejátszása
Mivel A kezdett, így 6 lépés után láthatjuk,
hogy B nyert, mivel A-nak már nincs helyes lépése. Harary és
Leary [6]-ban azt bizonyították be, hogy ha n páros,
akkor B nyer, ha n páratlan, akkor A nyer.
Hivatkozás
jegyzék
[1] Claude-Gasper Bachet: Problémes plaisant et detectables,1612
[2] Berger György: Bűvös négyzetek
Dacia Könyvkiadó, Kolozsvár, 1986.
[3] J. Chernick: Solution of the general magic square.
Amer. Math. Monthly 4(1938) 172-175
[4] J.Dénes, A.D. Keedwell: Latin squares and their applications. Academic
Press, New York, Akadémiai Kiadó, Budapest, English
Universities Press, London, 1974.
[5] A.H.Frost:The construction of Nasik squares of any order.Proc.
London Math.Soc. 27 (1985-96) 487-518
[6] F.Harary, T.Leary: Latin square schievment games. J.Recreational Math.16
(1983/84) 241-246
[7] D.King: Magic square puzzles. Frederich Müller Limited, London,1984
[8] Kiss Elemér: Matematikai kincsek Bolyai János kéziratos hagyatékából
Akadémiai Kiadó, Typotex Kiadó,
Budapest, 1999.
[9] M.Ozanam: Recreations mathematique et physiques. Tome 1-4.
Paris,Claude Joubert, 1723
[10] Poignard: Traité des Quarréa sublines contenent d Methodes Generales,
toutes Nouvelles e faciles, pour faire les sept Quarres
planetaires et tout autrea a l infine, Brüssel, 1794