![]()
D é n e s T a m á s matematikus
e-mail: tdenest@freemail.hu
![]()
Latin négyzetek alkalmazásai
a titkosításban
Girolamo Cardano (1501-1576) korszakos és mai napig ható módszercsaládja,
amely a sztegonográfia[1]
új ágát indította útjára, a róla elnevezett Cardano-rács.
A rács szó barátságtalan hangulatát feloldhatja, hogy tulajdonképpen itt egy betűmátrixra helyezhető sablonról van szó.
A pontosabb megértéshez idézzük fel magának Cardanonak a szavait:
"Végy két azonos méretű
pergamen lapot és azonos vonalak mentén készíts kivágásokat[2]
különböző helyeken. Ezek a kivágások legyenek kicsik, de mégis legalább
akkorák, mint az ABC nagybetűi. Az
összes kivágásokba összesen 120 betűt
lehessen elhelyezni. Az egyik pergamen lapot majd a levelező társadnak adod.
Amikor alkalom adódik, először írd az üzenetedet olyan tömören, ahogy csak
lehetséges, így az üzenet kevesebb betűt is tartalmazhat, mint amennyi a
kivágott ablakokban elhelyezhető. Amikor beírtad az üzeneted az egyik pergamen
lapra, tedd ugyanezt a másikkal is. Ezután töltsd ki az első lapon az üresen
maradt helyet úgy, hogy teljes mondatokra egészítsék ki a már ráirt szöveget.
Ez a kitöltés úgy történjen, hogy a teljes szöveg stílusa és tartalma
összefüggő és egységes legyen. Amikor a levelező társad megkapja a te
üzenetedet, ráhelyezi a megfelelő kivágásokkal ellátott pergament és így
elolvashatja az üzenetet."
A rejtjelző rács figyelemreméltó "divattá" vált évszázadokon
keresztül a kriptográfiában. A Cardano-rács történetét és alkalmazását a
titkosításban e folyóirat hasábjain már részletesen tárgyaltam (lásd [6]),
ezért jelen dolgozatomban a permutációs mátrixokkal és latin négyzetekkel való
kapcsolatát mutatom be, amely egyúttal rávilágít eme 450 éves találmány XXI.
századi rendkívüli lehetőségeire. A digitális technika új perspektívákat nyit a
sztegonográfiának és ezen belül a rejtjelző rácsoknak is.
Latin négyzetek és permutációs mátrixok
kapcsolata
Egy P(n) nxn-es, (0,1)-es mátrixot permutációs mátrixnak nevezünk, ha a mátrix pontosan n darab 1-t tartalmaz úgy, hogy minden sorban és oszlopban pontosan egy darab 1 lehet, a többi elem nulla.
Érdekes és a rejtjelző-rácsok szempontjából fontos eredmény az alábbi:
Egy L(n) nxn-es latin négyzet kölcsönösen-egyértelműen felbontható n darab permutációs mátrix összegére (lásd [2], [3]), azaz
(1) L(n)=![]()
ahol ![]() az
az ![]() -adik permutációs mátrix, azaz a mátrixban 1 szerepel mindenhol, ahol L(n)-ben k van, a mátrix
többi eleme nulla. (A "+"
összeadás művelet a mátrixok összeadását, míg a "
-adik permutációs mátrix, azaz a mátrixban 1 szerepel mindenhol, ahol L(n)-ben k van, a mátrix
többi eleme nulla. (A "+"
összeadás művelet a mátrixok összeadását, míg a "![]() " szorzás a mátrixok skalár szorzását jelöli.)
" szorzás a mátrixok skalár szorzását jelöli.)
Ezen megfeleltetések következménye, hogy az így adódó permutációs mátrixok jól felhasználhatók rejtjelző rácsként. A következő szemléltető példában a (2)-beli L(4) latin négyzet P1, P2, P3, P4 permutációs mátrixokra való egyértelmű felbontása látható:
(2) 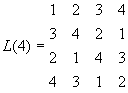
(3) 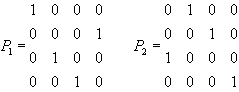
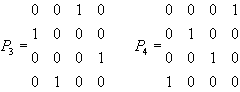
A rejtjelző rács tulajdonképpen egy betűkeverési rejtjelző eszköz,
amely az úgynevezett nyílt szöveg betűit egy betűmátrixba képezi le. Mindegyik
![]() permutációs mátrix
egy rejtjelző rácsként fogható fel, ahol az
1-esek helyén "ablakok" vannak.
permutációs mátrix
egy rejtjelző rácsként fogható fel, ahol az
1-esek helyén "ablakok" vannak.
Példaként legyen a nyílt szöveg a
"SZIA" és használjuk a ![]() permutációs mátrixot
rejtjelző rácsként. Ekkor egy tetszőleges B
4x4-es betűmátrixban hagyjuk üresen azokat a cellákat, ahol
permutációs mátrixot
rejtjelző rácsként. Ekkor egy tetszőleges B
4x4-es betűmátrixban hagyjuk üresen azokat a cellákat, ahol ![]() -ben 1-es van (ezek a
rejtő "ablakok").
-ben 1-es van (ezek a
rejtő "ablakok").
![]()
![]()
![]()
![]() (4) B=
(4) B= 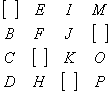
Majd az "ablakokba"
balról-jobbra, fentről-lefelé írjuk be a nyílt szöveget, így kapjuk a ![]() -nek megfelelő ráccsal rejtjelzett
-nek megfelelő ráccsal rejtjelzett ![]() betűmátrixot.
betűmátrixot.
(5) 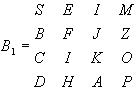
Így a permutációs mátrixok (mint
rácsok) egymás utáni betűmátrixra helyezésével tudjuk a kívánt szöveget a
betűmátrixba írni és a fordított eljárással kiolvasni. Mivel a latin
négyzetekre vonatkozó fenti egyértelmű felbontási tétel miatt az így készített
rácsok ablakai pontosan lefedik a betűmátrix
![]() mezőjét, ezzel a
módszerrel elértük, hogy a teljes betűmátrixot kitölthetjük rejtett szöveggel.
További előny, hogy a latin négyzet felbontásának egyértelműsége nem sérül, ha
a felbontást adó permutációs mátrixok (rácsok) sorrendjét megváltoztatjuk. Így
a felbontások számának n!-szorosa a lehetséges
rácsfelhasználások száma.
mezőjét, ezzel a
módszerrel elértük, hogy a teljes betűmátrixot kitölthetjük rejtett szöveggel.
További előny, hogy a latin négyzet felbontásának egyértelműsége nem sérül, ha
a felbontást adó permutációs mátrixok (rácsok) sorrendjét megváltoztatjuk. Így
a felbontások számának n!-szorosa a lehetséges
rácsfelhasználások száma.
A rejtjelzésben a kulcstér mérete is fontos tényező,
ezért igen érdekesek a latin négyzetek számára vonatkozó eredmények. Az
L(n) nxn-es latin négyzetek permutációs
mátrixokra való felbontásainak száma megegyezik az összes nxn-es latin
négyzetek számával. A latin négyzetek számára pontos formula egyelőre nem
létezik, azt azonban tudjuk, hogy
ha ![]() -nel jelöljük az úgynevezett redukált nxn-es latin négyzetek számát
(redukált latin négyzet, melynek első sora és oszlopa az 1,2,...,n természetes
számokat alapsorrendben tartalmazza), akkor
-nel jelöljük az úgynevezett redukált nxn-es latin négyzetek számát
(redukált latin négyzet, melynek első sora és oszlopa az 1,2,...,n természetes
számokat alapsorrendben tartalmazza), akkor
![]() , míg az összes nxn-es latin négyzetek számára fennáll
az
, míg az összes nxn-es latin négyzetek számára fennáll
az ![]() =n!(n-1)!
=n!(n-1)!![]() összefüggés. A redukált latin négyzetek számának pontos
értékét eddig csupán n=10-ig sikerült
számítógépes segítséggel meghatározni, hogy mekkora számokról van szó, annak
illusztrálására álljon itt
összefüggés. A redukált latin négyzetek számának pontos
értékét eddig csupán n=10-ig sikerült
számítógépes segítséggel meghatározni, hogy mekkora számokról van szó, annak
illusztrálására álljon itt ![]() = 377.597.570.964.258.816
(lásd [1]
). Ez a szám kb. 38 milliószorosa a Földön ma élő emberiség létszámának. A
rejtjelzésben javasolható rácsméretek az
= 377.597.570.964.258.816
(lásd [1]
). Ez a szám kb. 38 milliószorosa a Földön ma élő emberiség létszámának. A
rejtjelzésben javasolható rácsméretek az ![]() értékek!
értékek!
A következőkben megmutatjuk, hogy a permutációs mátrixok (és bizonyos feltételek mellett a latin négyzetek is) megsorszámozhatók, azaz az nxn-es permutációs mátrixok és az 1, 2, ..., n! természetes számok között kölcsönösen egyértelmű megfeleltetés létesíthető. Az 1., 2., 3. tételek bizonyítása megtalálható [4] és [5]-ben.
1.Tétel
Bármely ![]() nxn-es
permutációs mátrixhoz kölcsönösen egyértelműen hozzárendelhető egy
nxn-es
permutációs mátrixhoz kölcsönösen egyértelműen hozzárendelhető egy ![]() n-edfokú permutáció.
n-edfokú permutáció.
Az 1.tétel illusztrálásához lássuk el a (3)-beli P1 permutációs mátrixot perem elemekkel. Ekkor a (6) mátrixot kapjuk.
(6)
|
|
1 |
2 |
3 |
4 |
|
1 |
1 |
0 |
0 |
0 |
|
2 |
0 |
0 |
0 |
1 |
|
3 |
0 |
1 |
0 |
0 |
|
4 |
0 |
0 |
1 |
0 |
A ![]() permutációs mátrixhoz
rendeljük a p1 permutációt a következőképpen:
permutációs mátrixhoz
rendeljük a p1 permutációt a következőképpen:
- A P1 mátrix első sorában található 1-hez tartozó vízszintes és függőleges perem elemeket írjuk egymás alá, ez lesz a p1 permutáció első oszlopa.
-
Tegyük ugyanezt a P1
mátrix második, harmadik, negyedik sorával, így kapjuk a p1 permutáció megfelelő
oszlopait, azaz, ha P(i,j)=1, akkor p1
megfelelő oszlopa ![]() (lásd a (7)
levezetést)
(lásd a (7)
levezetést)
(7) 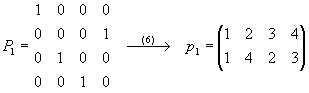
Permutációk és a
"faktoriális alapú" számrendszer
Ahhoz, hogy a permutációs mátrixokhoz sorszámot rendeljünk, az 1.tétel alapján elegendő a permutációk megsorszámozása. Erre ad módot a következő 2. és 3. tétel.
2.Tétel ("faktoriális alapú" számrendszer)
Legyenek m és ![]() természetes számok,
melyekre teljesül, hogy
természetes számok,
melyekre teljesül, hogy
(8) ![]()
(9) ![]() (i=1, 2, 3, ...,
n)
(i=1, 2, 3, ...,
n)
(10) ![]()
Ekkor bármely (8)-nak megfelelő m-hez pontosan egy ![]() sorozat létezik,
amely eleget tesz a (9), (10) összefüggéseknek.
sorozat létezik,
amely eleget tesz a (9), (10) összefüggéseknek.
Amint azt láttuk, az összes n-ed
rendű latin négyzet előállítása teljesen megoldatlan probléma, hiszen akkor
egyúttal megoldódna a leszámlálásuk is, de
![]() esetén még az összes
latin négyzetek pontos számát sem ismerjük. Így a latin négyzetek alkalmazása
szempontjából különleges jelentősége van, ha bizonyos típusú latin négyzet
osztályok előállítására tudunk algoritmust adni, főleg ha ez egyszerre a
természetes számokhoz való egyértelmű hozzárendelést is jelent. Ekkor ugyanis a
rejtjelzésben jelentőséggel bíró véletlenszám generátorok felhasználására is
mód nyílik, másrészt jelentős tárolási és továbbítási előnye van. A
következőkben olyan latin négyzet osztályt állítunk elő, amelynek soraiban lévő
permutációk elemi transzpozíciókkal származtathatók egymásból. Az algoritmus
részletes leírása [4], [5]-ben megtalálható.
esetén még az összes
latin négyzetek pontos számát sem ismerjük. Így a latin négyzetek alkalmazása
szempontjából különleges jelentősége van, ha bizonyos típusú latin négyzet
osztályok előállítására tudunk algoritmust adni, főleg ha ez egyszerre a
természetes számokhoz való egyértelmű hozzárendelést is jelent. Ekkor ugyanis a
rejtjelzésben jelentőséggel bíró véletlenszám generátorok felhasználására is
mód nyílik, másrészt jelentős tárolási és továbbítási előnye van. A
következőkben olyan latin négyzet osztályt állítunk elő, amelynek soraiban lévő
permutációk elemi transzpozíciókkal származtathatók egymásból. Az algoritmus
részletes leírása [4], [5]-ben megtalálható.
Az eljárás elemi transzpozíciók segítségével állítja elő a permutációkat. Legyen a kiindulási permutáció[3] :
(11) ![]()
Ekkor a rekurziós formula a következő:
(12) ![]()
![]() meghatározásához
soroljuk a természetes számokat az
meghatározásához
soroljuk a természetes számokat az ![]() osztályokba úgy,
hogy
osztályokba úgy,
hogy
![]() (13)
(13) ![]() és
és ![]()
![]()
![]()
(14) 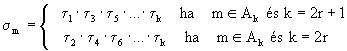
A ![]() transzpozíció
szorzatot a továbbiakban
transzpozíció
szorzatot a továbbiakban ![]() transzformációnak
nevezzük.
transzformációnak
nevezzük.
A ![]() jelölés elemi
transzpozíciót jelöl, azaz
jelölés elemi
transzpozíciót jelöl, azaz ![]() , így (14) a következőképpen írható:
, így (14) a következőképpen írható:
(15) 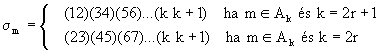
Az eljárás tehát a következő transzformáció szorzatot állítja elő:
(16) ![]() (k=1, 2, ..., n!-1)
(k=1, 2, ..., n!-1)
Osztályozzuk a transzformációkat az indexük szerint,
vagyis ![]() és
és ![]() akkor és csak akkor
tartozik egy osztályba, ha r
és s a (13)
definíció szerint egy osztályba tartozik. Ekkor könnyen belátható, hogy az egy osztályba tartozó
transzformációk egyenlők, hiszen r és
s egyértelműen határozzák meg a (15)
definíció k osztályindexét.
akkor és csak akkor
tartozik egy osztályba, ha r
és s a (13)
definíció szerint egy osztályba tartozik. Ekkor könnyen belátható, hogy az egy osztályba tartozó
transzformációk egyenlők, hiszen r és
s egyértelműen határozzák meg a (15)
definíció k osztályindexét.
A (13)-(16) osztályozási definíciók és a transzformációk egyenlősége miatt igaz a következő:
(17) 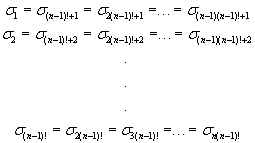
Helyettesítsük be (16)-ba a (17) egyenlőségrendszerben kapottakat:
(18) ![]()
Mivel a ![]() transzformáció
szorzat nem más, mint az összes
(n-1)-ed fokú permutációk előállításához szükséges transzformációk
szorzata, vezessük be a következő egyszerűbb jelölést:
transzformáció
szorzat nem más, mint az összes
(n-1)-ed fokú permutációk előállításához szükséges transzformációk
szorzata, vezessük be a következő egyszerűbb jelölést:
(19) ![]()
Ahol tehát ![]() az összes r-ed fokú permutáció előállításához
szükséges transzformációk szorzatát jelöli.
Ekkor (18) így írható:
az összes r-ed fokú permutáció előállításához
szükséges transzformációk szorzatát jelöli.
Ekkor (18) így írható:
(20) ![]()
Latin négyzetek
megszámozása
3. Tétel
A (20) formula n! különböző permutációt állít elő.
Következmények:
K3.1.
A 3.tétel következményeként adódik, hogy a (17)
egyenlőségrendszer minden sorának első eleme különböző permutációt állit elő. Az egy sorban levő
transzformációk a teljes n-edfokú
ciklus (![]() ) különböző hatványaival szorozzák a sor első (kezdő)
permutációját, így ezek is különbözőek és teljes ciklust alkotnak. Ebből
következik, hogy (17)
minden sora n darab olyan permutációt generál, amelyek egy
latin négyzetet alkotnak.
) különböző hatványaival szorozzák a sor első (kezdő)
permutációját, így ezek is különbözőek és teljes ciklust alkotnak. Ebből
következik, hogy (17)
minden sora n darab olyan permutációt generál, amelyek egy
latin négyzetet alkotnak.
K3.2.
Másrészről (17) minden sora különböző latin négyzetet állít elő, így a fenti rekurzív eljárással (n-1)! latin négyzet könnyen előállítható.
K3.3.
A K3.1. következményből adódik, hogy az így generált latin négyzetek reprezentálhatók a megfelelő sor kezdőpermutációjával. Azaz a kezdőpermutációhoz rendelt sorszámmal azonosíthatók. A fentiekben bevezetett jelölésekkel az alábbi sorszámozott latin négyzeteket kapjuk:
(21) 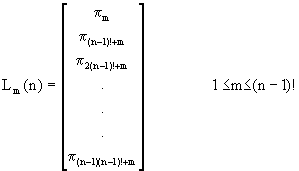
Példa: n=4, m=3 (lásd az 1.táblát)
(22) 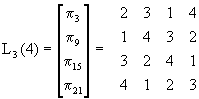
Az (1) felbontásnak megfelelően permutációs mátrixok összegeként felírva:
(23) ![]()
![]()
Példa: n=4, m=3 (lásd az 1.táblát)
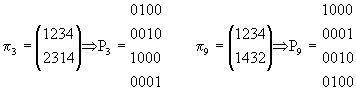
(24)
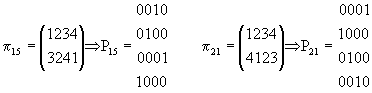
(25) 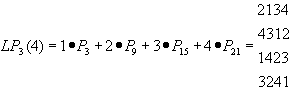
Latin négyzet alapú
rejtjelzés
Használjuk a példa permutációs mátrixait rejtjelző-rácsként. Legyen a nyílt szöveg "AMI TITOK AZ TITOK!" és legyen a rácsok sorrendje a fenti (3, 9, 15, 21), ekkor a rejtett betűmátrix a következő:
(26) 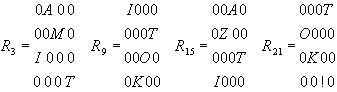
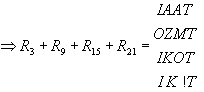
Mint azt megjegyeztük, ugyanezzel a négy ráccsal 4!=24-féleképpen állíthatjuk elő a rejtett betűmátrixot. Példaként bemutatjuk a 15, 3, 21, 9 sorrendhez tartozó betűmátrixot is:
(27) 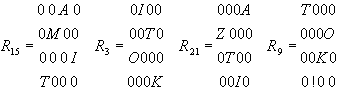
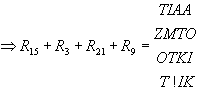
A fenti rekurziós algoritmus az összes n-edfokú permutációknak egy egymásbaskatulyázott blokkos elrendezését adja (lásd 1.tábla), amelyre teljesülnek az alábbi állítások:
A1. Minden blokk utolsó oszlopában azonos elemek vannak.
A2. Azonos fokszámú, de különböző blokkok utolsó oszlopai különbözők.
A3. Az A1., A2.
tulajdonságokból következik, hogy egy tetszőleges 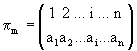 n-edfokú permutáció minden eleme
egyértelműen meghatároz egy blokkot, mégpedig az
n-edfokú permutáció minden eleme
egyértelműen meghatároz egy blokkot, mégpedig az ![]() elem egy (i-1)-edfokú blokkot, amelyhez hozzárendelhetjük a (9)
szerinti
elem egy (i-1)-edfokú blokkot, amelyhez hozzárendelhetjük a (9)
szerinti ![]() értéket. Az így
nyert
értéket. Az így
nyert ![]() (i=1,2,...,n) sorozat
(10) szerint egyértelműen
rendeli a permutációhoz az m
természetes számot.
(i=1,2,...,n) sorozat
(10) szerint egyértelműen
rendeli a permutációhoz az m
természetes számot.
1.táblázat
|
1. |
1 |
2 |
3 |
4 |
|
2. |
2 |
1 |
3 |
4 |
|
3. |
2 |
3 |
1 |
4 |
|
4. |
3 |
2 |
1 |
4 |
|
5. |
3 |
1 |
2 |
4 |
|
6. |
1 |
3 |
2 |
4 |
|
7. |
3 |
1 |
4 |
2 |
|
8. |
1 |
3 |
4 |
2 |
|
9. |
1 |
4 |
3 |
2 |
|
10. |
4 |
1 |
3 |
2 |
|
11. |
4 |
3 |
1 |
2 |
|
12. |
3 |
4 |
1 |
2 |
|
13. |
4 |
3 |
2 |
1 |
|
14. |
3 |
4 |
2 |
1 |
|
15. |
3 |
2 |
4 |
1 |
|
16. |
2 |
3 |
4 |
1 |
|
17. |
2 |
4 |
3 |
1 |
|
18. |
4 |
2 |
3 |
1 |
|
19. |
2 |
4 |
1 |
3 |
|
20. |
4 |
2 |
1 |
3 |
|
21. |
4 |
1 |
2 |
3 |
|
22. |
1 |
4 |
2 |
3 |
|
23. |
1 |
2 |
4 |
3 |
|
24. |
2 |
1 |
4 |
3 |
Ha a perrmutációs
mátrixokat rejtjelző-rácsként alkalmazzuk, akkor a ![]() mátrix, illetve az
ehhez tartozó
mátrix, illetve az
ehhez tartozó ![]() permutáció helyett
elegendő az i szám tárolása az azonosításhoz.
permutáció helyett
elegendő az i szám tárolása az azonosításhoz.
Egy n-ed fokú permutáció tárolásához (csak a képelemeket tároljuk!) c(n) számú karakterre van szükség, ahol
(28) ![]()
Az n! szám számjegyeinek száma (jelöljük j(n)-nel):
(29) ![]()
Ekkor bár fennáll, hogy
(30) 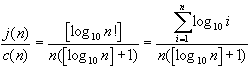
amelyre
(31) ![]()
mégis a gyakorlatban ez a
megfeleltetés jól használható, mivel az általában használatos ![]() értékekre a 2.táblázat értékei adódnak, ami azt mutatja,
hogy a gyakorlatban 25-50%
helymegtakarítást érhetünk el.
értékekre a 2.táblázat értékei adódnak, ami azt mutatja,
hogy a gyakorlatban 25-50%
helymegtakarítást érhetünk el.
2.táblázat
n j(n) c(n) ![]()
![]()
10 7 20 .35
100 158 300 .526
200 375 600 .625
300 614 900 .682
400 869 1200 .724
500 1134 1500 .756
![]()
Latin négyzet alapú
digitális aláírás
Az elektronikus pénz átutalás (EFT=Electronic Fund Transfer) és általában az elektronikus posta elterjedése felvetette a hagyományos aláírás helyettesítését digitálisan előállított (kódolt) elektronikus aláírással. A számítógépes terminálok használóinak, vagy az adatbankokhoz való hozzáférés jogosságának ellenőrzésénél hasonló problémákat kell megoldani, mint a hagyományos levél, illetve más papír alapú dokumentumok hitelesítésénél, ahol ezt a célt szolgálta a kézi aláírás. Nyilvánvaló, hogy egy digitális, teljesen elektronizált rendszerben a kézi hitelesítést is helyettesíteni kell, erre való a digitális aláírás, amely azonban olyan kódolási módszereket használ, amelyek nem csupán a dokumentum aláíróját, hanem a dokumentum tartalmát is hitelesítik.
Sok módszer ismeretes a digitális aláírás megvalósítására. Most egy olyan eljárást mutatok be, amely latin négyzeteken alapul és közvetlenül alkalmas párhuzamos működésű számítógépen való implementálásra, ami rendkívüli módon megnöveli a működési sebességet.
Legyen adott egy U=a1, a2,…, an üzenet ahol az üzenet betűi (ai ) egy q elemű ábécéből valók. Az üzenet hitelesítését (digitális aláírását) az üzenettel azonos ábécé-ből vett s darab (A=b1, b2,…, bs) betűvel kívánjuk elvégezni. Tegyük fel az egyszerűség kedvéért, hogy n osztható s-sel, vagyis n=s·t. Válasszuk szét az üzenetet s darab részüzenetre (a szétválasztás egy kulcs szerint fog történni, ami esetünkben egy latin négyzet).
Minden részüzenet t darab betűből fog állni és minden egyes részüzenet az elektronikus aláírás egy betűjét határozza meg.
Az eljárást egy példán fogom szemléltetni, amely a könnyebb áttekinthetőség érdekében kis n és q értékekre vonatkozik. Legyen az üzenet U=1032203101231003 (vagyis n=16, q=4, s=4). A kulcs amely szerint az üzenetet részüzenetekre bontjuk egy s-ed rendű (jelen esetben 4-ed rendű) latin négyzet:
|
0 |
2 |
3 |
1 |
|
2 |
1 |
0 |
3 |
|
1 |
3 |
2 |
0 |
|
3 |
0 |
1 |
2 |
(32)
A (33) mátrix egy
segédtáblázat, amelynek felhasználása a következőkben kerül ismertetésre.
|
1 |
2 |
3 |
4 |
|
5 |
6 |
7 |
8 |
|
9 |
10 |
11 |
12 |
|
13 |
14 |
15 |
16 |
(33)
Az
U üzenet U1, U2, U3, …, Us
részüzenetekre való bontásának lépései a következők:
Válasszuk
ki a (32) latin négyzetben szereplő azonos elemek sorszámát a (33) mátrix szerint úgy, hogy pl. a 0 elemekhez tartozó sorszámok a (33)
mátrix ráhelyezésével a következőknek adódnak: 1, 7, 12, 14. Ugyanezt az
eljárást alkalmazva a (32) latin négyzet 1-es, 2-es és 3-as elemeire is, a
sorszámokat négy osztályba osztjuk: (1, 7, 12, 14), (4, 6, 9, 15), (2, 5, 11,
16), (3, 7, 9, 13).
Ezután a sorszámokat (megtartva az osztályozást) helyettesítjük az U üzenetnek az illető sorszám szerinti helyén álló elemével. Így a következő kevert részüzeneteket kapjuk: U1= (1, 3, 3, 0), U2= (2, 0, 0, 0), U3= (0, 2, 2, 3), U4= (3, 1, 1, 1). Most lássuk el a (32) latin négyzetet perem elemekkel:
|
|
0 |
1 |
2 |
3 |
|
0 |
0 |
2 |
3 |
1 |
|
1 |
2 |
1 |
0 |
3 |
|
2 |
1 |
3 |
2 |
0 |
|
3 |
3 |
0 |
1 |
2 |
(34)
Így tulajdonképpen a
(0,1,2,3) halmazon definiáltunk egy * műveletet, amelynek művelettáblája a (34)
latin négyzet. A (34) művelettáblát pontosan úgy használjuk, mint a jól ismert
szorzótáblát, például azt kapjuk, hogy 0*1=2, 1*2=0, stb.
A nem matematikus olvasó számára talán szokatlan, hogy a * művelet nem asszociatív, vagyis a*(b*c) ¹ (a*b)*c, azaz például 2*(3*1)=2*0=1, de (2*3)*1=0*1=2, vagyis 2*(3*1) ¹ (2*3)*1. Ennek a tulajdonságnak nagy jelentősége van a következőkben bemutatott kódolási eljárásnál.
A példánkban szereplő U üzenet digitális aláírásához az egyes U1, U2, U3, U4 részüzenetek szorzatát kell előállítani a (34) művelettábla alapján:
b1 = ((1*3)*3)*0 = (3*3)*0=2*0= 1
(35) b2 = ((2*0)*0)*0 = (1*0)*0=2*0= 1
b3 = ((0*2)*2)*3 = (3*2)*3=1*3= 3
b4 = ((3*1)*2)*1 = (0*1)*1=2*1= 3
vagyis az U üzenethez tartozó hitelesítő aláírás: A=(b1b2b3b4)= 1133
A fenti eljárás teljesen egyértelmű eredményre vezet, hiszen az U üzenet felbontása részüzenetekre a latin négyzet elemeinek diszjunkt osztályozásán alapul, ez viszont a fentiekben ismertetett permutációs mátrixokra való felbontási tétel miatt kölcsönösen egyértelmű. A latin négyzeteken alapuló művelettáblák nem asszociatív algebrai struktúrát (úgynevezett kvázicsoportot) reprezentálnak, aminek nagy jelentősége van az illetéktelen hamisítás elleni védekezésnél, mivel két karakter egyszerű felcserélését is kimutatja. Ezzel a képességgel a paritás ellenőrzésen alapuló módszerek, vagy a numerikus eljárások nem rendelkeznek.
Záró
megjegyzésként szeretném felhívni az olvasó figyelmét arra, hogy a rejtjelzés,
hitelesítés, digitális aláírás numerikus módszereinek biztonsága
(feltörhetősége) alapvetően függ a pillanatnyi számítástechnikai eszközök
kapacitásától. Azaz a feltörhetetlenség mellett szóló érvek, a több ezer éves
számolási igény a rejtett kulcsok megfejtéséhez, a gyors hardver fejlődéssel
bizonytalanná válnak.
Bízom benne, hogy a latin négyzetek titkosítási alkalmazásainak e
vázlatos ismertetéséből egyértelműen kitűnik, hogy a latin négyzeteken alapuló
strukturális módszerrel aláírt és rejtjelzett elektronikus dokumentumok esetén
nem kell tartani a számítógépek sebesség és kapacitás növekedésétől!
Hivatkozások jegyzéke
[1] J.Dénes, A.D.Keedwell: Latin squares and their applications
Akadémiai Kiadó, Budapest, 1974.
[2] J.Dénes, A.D.Keedwell: Latin squares and 1-factorizations of complete graphs I.
Ars Combinatorica, 25A (1988), pp. 109-126.
[3] J.Dénes, A.D.Keedwell: Latin squares and 1-factorizations of complete graphs II.
Utilitas Math., 34 (1988), pp. 73-83.
[4] Dénes Tamás: Algoritmusok az összes n-edfokú permutáció előállítására I.
Információ Elektronika, 1975.1.
[5] Dénes Tamás: Algoritmusok az összes n-edfokú permutáció előállítására II.
Információ Elektronika, 1975.2.
[6] Dénes Tamás: A Rejtjelző Rácsok Születése
Híradástechnika, 2001/10. 57-63
[7] Dénes Tamás: SZTEGONOGRÁFIA - rejtett információk rejtjelzés nélkül
Híradástechnika, 2001/8. 15-21