Estimation
of the number of twin primes by application of
the Complementary Prime Sive
T a m á s D é n e s mathematician
free-lance
expert
e-mail: tdenest@freemail.hu
Published
in the journal PU.M.A. Vol. 13 (2002), No. 3.
--- . ---
Abstract. In the
[1] paper we introduced the „Complementary Prime-Sieve” (C.P.S.) which gives
necessary and sufficient conditions to generate composite numbers larger than 3
of the forms 6k-1 and 6k+1. Here we
give a proof of S.W.Golomb’s Theorem (see [3]) about the numbers of twin
primes, then we deduce an approximate formulae for the T(N) numbers of twin
primes in the 1-N interval, also based on C.P.S.
Mathematics Subject Classifications (2000). 11A07, 11A41, 11A51
1.
Necessary and sufficient condition for the twin prime theorem
Theorem
1.
are twin primes iff 
where k=1,2,3,...
Proof:
According to the Theorem 1. in [1] (Every prime numbers larger than 3 are of the forms 6k+1 or 6k-1) there are two options:
(1)
p=6k-1 
q=p+2=6k+1
(2) p=6k+1 
q=p+2=6k+3=3(2k+1)
but this is not a prime.
Consequently,
only case (1) is possible. Inversely the proof is trivial.
Q.E.D.
Corollary
1.
(3) pq =
(6k-1)(6k+1) = 
if p,q
are twin primes. This implies the Theorem 2. below:
Theorem
2.
(
) has two prime factors iff
6k-1 and 6k+1 are twin primes.
Proof:
If (
) has exactly two prime factors, then according to (3) these
can only be 6k-1 and 6k+1. Thus 6k-1 and 6k+1 are twin primes.
If 6k-1 and 6k+1
are twin primes, then also according to (3), (
) cannot have other prime factors.
Q.E.D.
Theorem
2. implies the theorem below regarding about the cardinality of twin primes:
The cardinality of twin primes is finite iff there
is a K natural number for which, every 
implies that (36k2
–1) have at least three prime factors.
It can be realized only if at least one of 6k-1 and 6k+1 is a composite
number. According to the Theorem 2. in [1] (C.P.S. theorem) it is possible
iff k can be described as one of
the following forms:
(4) k=6uv+u+v or k=6uv-u-v or
k=6uv-u+v or k=6uv+u-v
With these states we have proved the Theorem 3.
below:
Theorem
3.
The cardinality of twin primes is finite iff there
is a K natural number for which every
can be written into
one of the forms (4).
In this way we have also proved S.W.Golomb’s theorem which he introduced in [3] as an E969 open problem :
„A necessary and sufficient condition that there be infinitely many twin primes is there be infinitely many numbers k not of the forms (4).”
2. Estimation of the number of twin primes in the
interval (1-N)
Let us order the natural numbers of the forms 6k-1
and 6k+1 according to Table 1. It can
be seen easily that Table 1. contains all the natural numbers of the form 6k-1
in the second column and all the natural numbers of the form 6k+1 in the third
column, so all the prime numbers as well.[1]
According to the Theorem 1. (see above) all the twin
primes are in those lines of the table where there are prime numbers in the
second and the third column as well. Thus the meaning of Theorem 3. is that
in rows after K of Table 1. only one of the numbers can possibly be a prime
number. Thus every k
K row index can be put into one
of the forms (4).
Table 1.
|
k
|
6k-1
|
6k+1
|
|
|
1
|
5
|
7
|
twin prime
|
|
2
|
11
|
13
|
twin prime
|
|
3
|
17
|
19
|
twin prime
|
|
4
|
23
|
25
|
 |
|
5
|
29
|
31
|
twin prime
|
|
6
|
35
|
37
|
 |
|
7
|
41
|
43
|
twin prime
|
|
8
|
47
|
49
|
 |
|
9
|
53
|
55
|
 |
|
10
|
59
|
61
|
twin prime
|
|
11
|
65
|
67
|
 |
|
12
|
71
|
73
|
twin prime
|
|
13
|
77
|
79
|
 |
|
14
|
83
|
85
|
 |
|
15
|
89
|
91
|
 |
|
16
|
95
|
97
|
 |
|
17
|
101
|
103
|
twin prime
|
|
18
|
107
|
109
|
twin prime
|
|
19
|
113
|
115
|
 |
|
20
|
119
|
121
|
 |
|
...
|
...
|
...
|
|
|
K
|
6K-1
|
6K+1
|
|
|
...
|
...
|
...
|
Now, we will show that in Table 1. there are rows in
which there are certainly not any twin primes. Firstly we examine the cases
k=5r, k=5r+1, k=5r+2, k=5r+3, k=5r+4, which cases obviously generate all k
row indexes.
-If
k=5r (r=1,2,3,...), then 6k-1=30r-1
and 6k+1=30r+1
These two
sequences contain each fifth row of the Table 1. where there are twin primes
for example in the following (see Table 1.):
r= 1, 2, 5,
6,... k=
5, 10, 25, 30,...
-If k=5r+1 (r=1,2,3,...), then 6k-1=30r+5=5(6r+1) which is not a prime
number, so these rows definitely don’t contain twin primes (see Table 1.). For
example: r=1, 2, 3, 4,...
k=6, 11, 16, 21,...
-If k=5r+2
(r=0,1,2,3,...), then 6k-1=30r+11 and
6k+1=30r+13
These two
sequences also come up in each fifth rows of Table 1. starting from the second
row, where there are twin primes. For example (see Table 1.): r=0,
1, 2, 3, 6,... k=2, 7, 12,
17, 32,...
-If k=5r+3
(r=0,1,2,3,...), then 6k-1=30r+17 and
6k+1=30r+19
These two
sequences also come up in each fifth rows of Table 1. starting from the 3rd
row, where there are twin primes. For example (see Table 1.): r=0,
3, 4, 6,... k=3, 18, 23, 33,...
-If k=5r+4
(r=0,1,2,3,...), then 6k-1=30r+23 and
6k+1=30r+25=5(6r+5), which is not a prime number, so in these rows there
will certainly not be any twin primes.
According to the above mentioned in the rows k=5r+1,
and k=5r+4 of Table 1. there are not any twin primes (k=4,6,9,11,14,16,...) thus
(5) all the twin primes are
contained in the k=5r, k=5r+2,
k=5r+3 (k=0,1,2,3,...) rows of the Table 1.
Consequently there is an upper bound for the number
of twin primes (denote T(N)):
The number of rows in Table 1. to N (denote 
) is: 
According to the previous deduction twin primes can
occur in maximum 
part of these rows:
(6) T(N)
Let us examine the rows of the forms (5) of Table 1. with the aid of C.P.S.
There are definitely not any twin primes in rows
(5), if the k rowindex can be
put into one of the forms of (4). Because the (4) relations are symmetric for
u,v we can examine the cases when u=constant.
(7) u=1 and k=5r= 6uv+u+v 
k=7v+1 holds, if
v=5a+2 
k=35a+15
(8) u=1 and k=5r= 6uv-u-v 
k=5v-1 
5r=5v-1, it can
never be realised
(9) u=1 and k=5r= 6uv+u-v 
k=5v+1 
5r=5v+1, it can
never be realised
(10) u=1 and k=5r= 6uv-u+v 
k=7v-1 holds, if v=5a+3, 
k=35a+20
(11) u=1 és k=5r+2= 6uv+u+v 
k=7v+1 holds, if v=5a+3, 
k=35a+22
(12) u=1 és k=5r+2= 6uv-u-v 
k=5v-1 
5r=5v-3, it can
never be realised
(13) u=1 és k=5r+2= 6uv+u-v 
k=5v+1 
5r=5v-1, it can
never be realised
(14) u=1 és k=5r+2= 6uv-u+v 
k=7v-1 holds, if
v=5a+4, 
k=35a+27
(15) u=1 és k=5r+3= 6uv+u+v 
k=7v+1 holds, if v=5a+1, 
k=35a+8
(16) u=1 és k=5r+3= 6uv-u-v 
k=5v-1 
5r=5v-4, it can
never be realised
(17) u=1 és k=5r+3= 6uv+u-v 
k=5v+1 
5r=5v-2, it can never
be realised
(18) u=1 és k=5r+3= 6uv-u+v 
k=7v-1 holds, if
v=5a+2, 
k=35a+13
As a consequence of deductions (7), (10), (11), (14), (15), (18) there are
not any twin primes in 
part of rows (5)
containing twin primes. In such a way we can make formulae (6) more precisely:
(19) T(N)
The case
u=2 leads us to the general
formulae.
(20) u=2 and k=5r= 6uv+u+v 
k=13v+2 holds,
if v=5a+1, 
k=65a+15
(21) u=2 and k=5r= 6uv-u-v 
k=11v-2 holds,
if v=5a+2, 
k=55a+20
(22) u=2 and k=5r= 6uv+u-v 
k=11v+2 holds,
if v=5a+3, 
k=55a+35
(23) u=2 and k=5r= 6uv-u+v 
k=13v-2 holds,
if v=5a+4, 
k=65a+50
(24) u=2 and k=5r+2= 6uv+u+v 
k=13v+2 holds, if
v=5a, 
k=65a+2
(25) u=2 and k=5r+2= 6uv-u-v 
k=11v-2 holds,
if v=5a+4, 
k=55a+42
(26) u=2 and k=5r+2= 6uv+u-v 
k=11v+2 holds,
if v=5a, 
k=55a+2
(27) u=2 and k=5r+2= 6uv-u+v 
k=13v-2 holds,
if v=5a+3, 
k=65a+37
(28) u=2 and k=5r+3= 6uv+u+v 
k=13v+2 holds,
if v=5a+2, 
k=65a+28
(29) u=2 and k=5r+3= 6uv-u-v 
k=11v-2 holds, if
v=5a, 
k=55a-2
(30) u=2 and k=5r+3= 6uv+u-v 
k=11v+2 holds,
if v=5a+1, 
k=55a+13
(31) u=2 and k=5r+3= 6uv-u+v 
k=13v-2 holds, if
v=5a, 
k=65a-2
Connections (20)-(31) show that starting from a certain row (which rows are
all different) each 55th and 65th rows definitely do not contain twin primes.
That is according to (19), 
part of the rows
containing twin primes potentially fall out as well. We can see that it’s true
for any u in general that su
part of the rows containing twin primes potentially definitely do not contain
twin primes, where
(32) 
We showed in C.P.S. method that if we want to
generate prime numbers until N then we have to „run” u from 1
until 
. Thus, the number of rows without twin primes below 1-N is:
(33) 
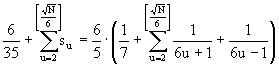
But of the statement explained in C.P.S. method, all
the u,v pairs generate k
by m(N) multiplicity in K(N)
steps. Thus, the number of rows not containing twin primes (denote S(N)) is the
following:
(34) S(N)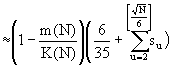 
This causes the estimation from (19) to T(N) below:
(35) T(N)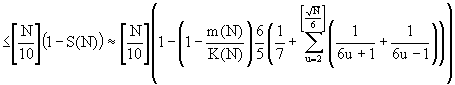
(36) 
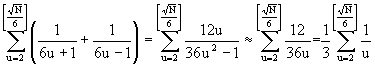
We use the estimated formulae below (see [2]
2.pp.):
(37) 
(38) 
From (38) and (36) the result is the following:
(39) 
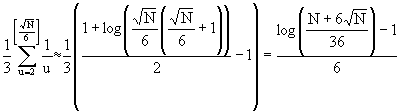
(40) 
= 
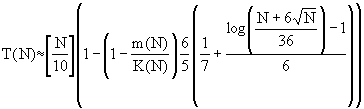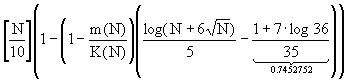
(41)
(42) 
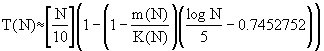
The result of Hardy and Littlewood (see [4]) for the
number of twin primes until x is the following (x is an arbitrary
natural number and T(x) the number of twin primes until x):
(41)
T(x)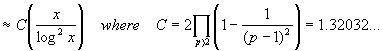
where 
means the prime
numbers are greater than 2 until x.
Let us denote the real number of twin primes
until N to RT(N). Than the comparison of the results above are contained in
Table 2.
Table 2.
|
N
|
 |
RT(N)
|
T(N)
|
|
T(x)
|
T(x) rel.err.
(%) |
|
100
|
0.1
|
8
|
8
|
-
|
6
|
25
|
|
1.000
|
0.165
|
35
|
42
|
20
|
27
|
23
|
|
2.000
|
0.23
|
61
|
75
|
22
|
45
|
26
|
|
3.000
|
0.27
|
81
|
101
|
24
|
61
|
25
|
|
4.000
|
0.29
|
103
|
131
|
27
|
76
|
26
|
|
5.000
|
0.30
|
126
|
156
|
23
|
90
|
29
|
|
10.000
|
0.35
|
205
|
268
|
30
|
155
|
24
|
|
30.000
|
0.42
|
467
|
660
|
41
|
372
|
21
|
|
50.000
|
0.44
|
705
|
964
|
36
|
563
|
21
|
|
1.000.000
|
0.56
|
8.169
|
9.774
|
19
|
6.915
|
16
|
|
2.000.000
|
0.58
|
14.871
|
16.102
|
8
|
12.541
|
16
|
|
3.000.000
|
0.59
|
20.933
|
20.734
|
1
|
17.803
|
15
|
|
4.000.000
|
0.60
|
26.861
|
27.451
|
2
|
22.847
|
15
|
|
5.000.000
|
0.61
|
32.464
|
31.398
|
3
|
27.739
|
15
|
|
8.000.000
|
0.62
|
48.619
|
46.103
|
5
|
41.797
|
14
|
Acknowledgment
I am happy to thank Dr S.W.Golomb for the informative letter in
which he explained that he has published the theorem in [3]: "A necessary and sufficient condition
that there be infinitely many twin primes is that there be infinitely many
numbers n not of the form 
." and he
wrote up-to-date historical background to it.
[1] T.Dénes:
Complementary prime-sive,
[2] P. Erdős, J. Surányi: Selected chapters from the theory of numbers
[3] S.W.Golomb: Problem E969: American Math.
Monthly, (vol 58. no.5. p 338.) 1951.
[4] S.W. Golomb:
The Twin Prime Constant
[5] W.Sierpinski: A Selection of Problems in the Theory of Numbers
[6] Maria Suzuki: Alternative Formulations of the Twin Prime Problem